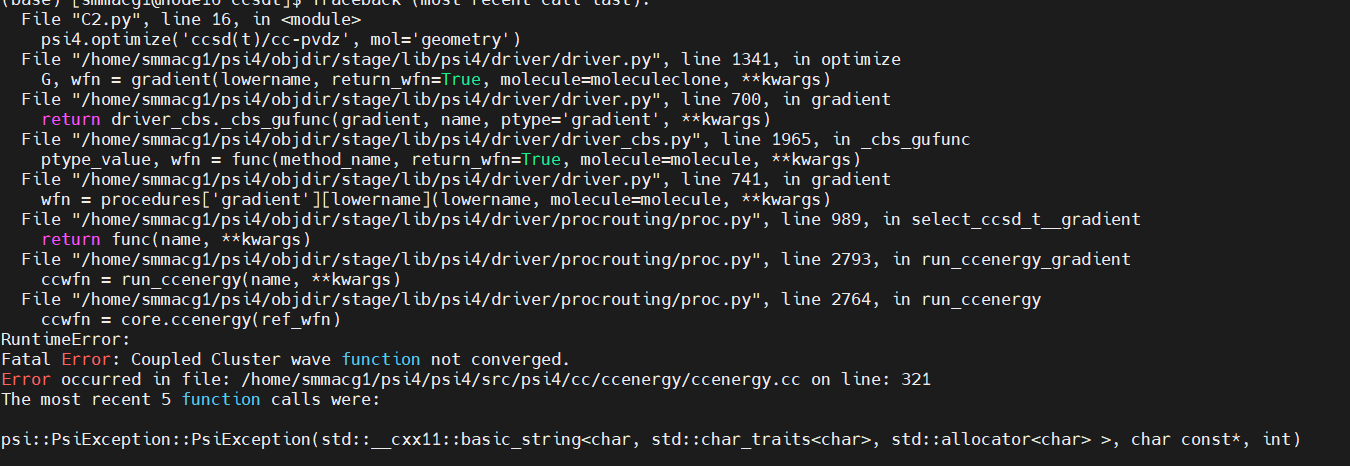
I have been trying to optimise C-3 carbon cluster using CCSD(T) using the following code:
import psi4
jobname = ‘C3’
psi4.core.set_output_file(jobname+‘.out’)
psi4.set_memory(“120 GB”)
psi4.set_num_threads(28)
geometry = psi4.geometry(“”"
C -5.000000000 -1.717572431 -4.971384315
C -2.830898467 -0.247075192 -5.000000000
C -3.915449220 -0.982323837 -4.985692161
“”")
psi4.optimize(‘ccsd(t)/aug-cc-pvdz’, mol=‘geometry’)
psi4.frequencies(‘ccsd(t)/aug-cc-pvdz’, mol=‘geometry’)
geometry.save_xyz_file(jobname+‘.xyz’, 1)
but it crashes with the error
Is this cluster supposed to be linear?
Yes the cluster is linear
The simplest solution is to change your input geometry so that it looks something like
C 0 0 0
C 0 0 2
C 0 0 4
That will both prevent the error and make your computations faster, because Psi4 can tell immediately that this is supposed to be a linear molecule.
Then what if I want to calculate the single point energy of a linear molecule of a particular geometry
Add “symmetry c1” to disable the error message entirely, at the cost of not taking advantage of symmetry.
(The trouble is that your molecule right now is not exactly linear, but it’s close enough to confuse Psi.)
So to be clear, if I were to add “symmetry c1”, then the calculated single point energy wouldn’t be of the given geometry but rather a different one
I don’t understand the question. “symmetry c1” disables Psi’s use of symmetry technology. It has nothing to do with changing the geometry.
Psi does reorient and re-center the input molecule, but that has nothing to do with your original question.
I have obtained the above co-ordinates for C-3 cluster after optimisation by means of using a global optimisation technique. Now I want to calculate the single point energy of this specific co-ordinate and also the optimised energy using CCSD(T) . This is my original problem. I apologise for the confusions created.
Then add “nocom” and “noreorient” to your molecule specification.
That said, your global optimization is unnecessarily complicated. You should have just set up your geometry like I described earlier. Then you would have had a 1D optimization problem. By not doing that, you allowed numerical noise to persist in other dimensions, and that is why you got your original error.
I did global optimisation as a part of my research project. In order to confirm that the geometry that I have obtained is indeed the global minima I am trying to do CCSD(T)
I’m very confused.
You opened this topic with a specific question about Psi4. The first sentence of my last post answered that question. You did not respond to it. Do you still have a specific question about Psi4?
As for your research project, what level of theory did you do your “global optimization” at? And you are aware that the Cartesian coordinates of the minimum are never unique, yes?
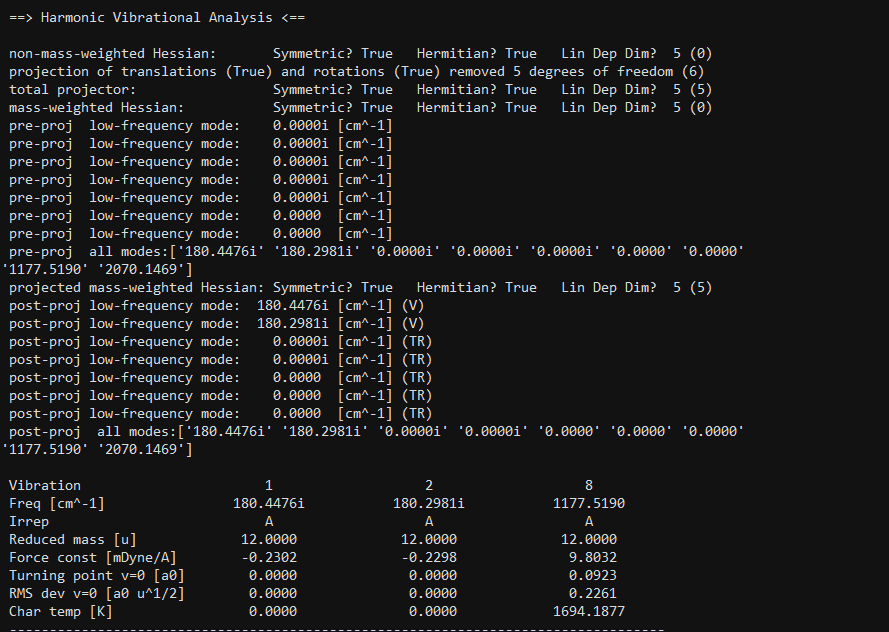
I used “symmetry c1” for the optimisation of the above co-ordinates and obtained the output file. The output file shows imaginary frequencies
Okay. What’s the question?
Usually after optimisation in gaussian16 we check for imaginary frequency in the output file. We remove the imaginary frequency by giving a manual displacement to some of the atoms in the molecule and resubmit the file for optimisation till we get zero imaginary frequency. Is there a way to do so in psi4
We give you the final optimized geometry, we give you the Cartesian coordinates for the imaginary frequency, and you can start an optimization from any starting geometry. So, yes, you can do this in Psi4.
I don’t understand why you would even question whether this is possible in Psi4. Just skimming the output file should have told you that you have all the pieces you need. Am I missing something?
Thank you for the reply. I am kind of new to psi4 . The main thing that I don’t understand is that from whatever geometry that I trying to reach the optimised geometry I am recieving imaginary frequencies. And as for the optimisation of the C2 carbon cluster using CCSD(T) and cc-pVDZ , the optimum geometry cannot be obtained due to convergence error. I even tried simplifying the co-ordinates as you said in the first post.
I need you to stick to one question at a time. I’m getting too confused trying to deal with multiple questions at once.
What is that one question? You’re saying that you’re always getting imaginary frequencies, no matter what your starting geometry?
I am getting 3 issues when I am trying to optimise a geometry. I will address the first issue.
Yes , I am getting imaginary frequencies no matter whatever is the starting geometry by using CCSD(T) cc-pVDZ
Can you clarify? Does this mean that the optimization simply returns to the same structure even after you displace it along the normal mode corresponding to the imaginary vibrational frequency? Have you tried scaling the displacement so that the structure is bent further away from linearity?