Dear PSI4 community,
I am not an expert in quantum chemical calculations. My objective is to adapt certain textbook plots to use them in teaching “General Chemistry”.
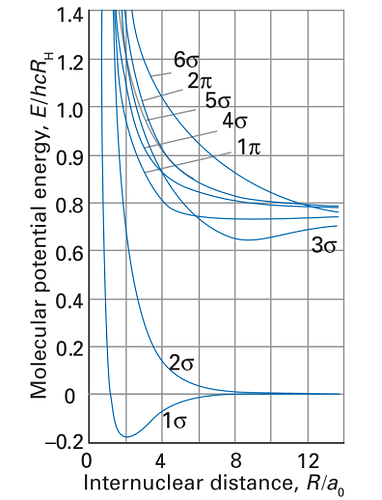
In particular, I would like to use PSI4 to calculate the total energy-distance curves for the hydrogen molecule H2. I succeed in obtaining the curve for the ground state (see the attached code which has been put together with the help of the available PSI4 tutorials). I can also directly obtain the energies of the molecular orbitals (not shown in the code), but what is needed is the total energy at a certain distance under the assumption that the electrons occupy higher orbitals.
Any suggestions on how I could obtain these values are greatly appreciated.
Thank you very much.
ps. The plot I would like to adapt is taken from Atkins / Friedmann (Molecular Quantum Mechanics).
import numpy as np
import pandas as pd
memory 600 mb
molecule h {
H
}
set reference uhf
h_energy, h_wfn = energy("ccsd(t)/cc-pVDZ", base_type="cp", return_wfn=True)
molecule h2 {
H
H 1 R
}
Rvals = np.linspace(0.15,3.5,50)
set reference rhf
rows = []
table = []
for R in Rvals:
h2.R = R
h2_energy, h2wfn = energy("ccsd(t)/cc-pVDZ", base_type="cp", return_wfn = True)
bonding = psi_hartree2kJmol * (h2_energy - 2*h_energy)
rows.append(R)
table.append([bonding])
df = pd.DataFrame(table, columns = ["bonding"], index = rows)
df.to_csv("h2.csv")