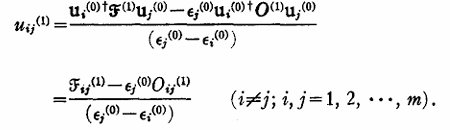Hello,
It seems orbital gradients with respect to position obtained using the code from scfgrad/response.cc do not match those computed using finite difference. Testing with an ethylene molecule and the following settings:
molecule {
0 1
C 1.52170169 3.49733377 1.50961816
C 0.60330749 4.06268597 2.43726659
H 1.78690064 2.42928720 1.40136826
H 1.74186659 4.13482666 0.72012866
H 0.41950327 5.09473991 2.55605364
H 0.09161823 3.49414158 3.08721519
units angstrom
no_reorient
}
set {
basis cc-pvdz
scf_type pk
reference rhf
}
hessian('hf')
and modifying the response.cc code to print out the CPHF “U” matrices (with the following code placed after line 2222 in response.cc):
{
auto Upi = std::make_shared<Matrix>("U", nmo, nocc);
double** Upip = Upi->pointer();
psio_address next_Upi = PSIO_ZERO;
for (int A = 0; A < 3 * natom; A++) {
psio_->read(PSIF_HESS, "Upi^A", (char*)Upip[0], static_cast<size_t>(nmo) * nocc * sizeof(double), next_Upi,
&next_Upi);
for (int k1=0; k1 < nmo; k1++) {
for (int k2=0; k2 < nocc; k2++) {
std::cout << *&Upip[k1][k2] << "\n";
}
}
}
}
and then computing the first order MO gradient wrt position using the printed out coefficients through some python code (where c contains the “zeroth order” MO coefficients from a SCF calculation):
import numpy as np
c = np.loadtxt("psi4_c.txt")
c = c.reshape(48, 48)
U = np.loadtxt("psi4_u.txt")
U = U.reshape(-1, 48, 8)
c_dr = np.einsum('pq,xqi->xpi', c, U).reshape(-1,3,48,8)
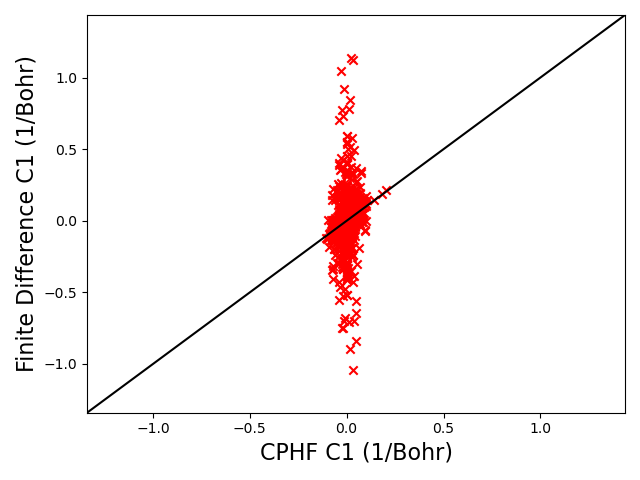
We can then compare the c_dr values computed above with the values computed using finite difference:
I believe the issue lies in the values used for the occupied-occupied block in the U matrices. On lines 2209-2215 in response.cc, the following code is being used to set the values for the occupied-occupied block U values:
for (int A = 0; A < 3 * natom; A++) {
psio_->read(PSIF_HESS, "Sij^A", (char*)Upqp[0], static_cast<size_t>(nocc) * nocc * sizeof(double), next_Spi,
&next_Spi);
C_DSCAL(nocc * (size_t)nocc, -0.5, Upqp[0], 1);
psio_->read(PSIF_HESS, "Uai^A", (char*)Upqp[nocc], static_cast<size_t>(nvir) * nocc * sizeof(double),
next_Uai, &next_Uai);
psio_->write(PSIF_HESS, "Upi^A", (char*)Upqp[0], static_cast<size_t>(nmo) * nocc * sizeof(double), next_Upi,
&next_Upi);
This corresponds to equations 41 and 42 in J. Chem. Phys. 49, 1719–1729 (1968) (https://doi.org/10.1063/1.1670299):
![]()
![]()
where the U values are set to -1/2 of the MO transformed first order overlap matrix gradient wrt position. It looks like you can set u_ij^1 = u_ji^1 = -1/2O_ji^1 for all occupied orbitals if they are real, and that’s what the code above is doing. However, this is only valid in the case where i = j. Examining Equation 40a in the above paper shows u_ij will not equal u_ji except in the case of a degeneracy:
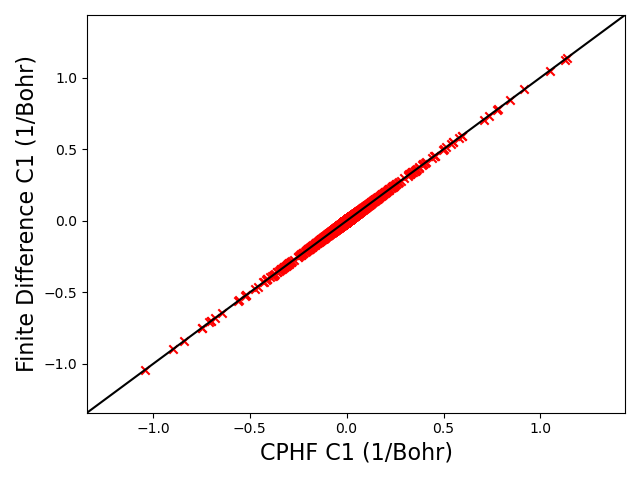
I belive the proper procedure to get the correct U matrices is to first solve for the occupied-virtual block of the U matrices (as is already being done in response.cc). This fully determines the MO transformed first order fock matrix gradient in Equation 40a. Then Equation 40a can be used to calculate the occupied-occupied u values for the cases where i is not equal to j, and then Equation 42 can be used for the cases where i = j. I made a github fork with code that does this for RHF Hessians, although it’s kind of messy and leaves an error with the U matrices unfixed psi4/psi4/src/psi4/scfgrad at master · jstoppelman/psi4. Printing out the U matrices from this version of the code, recalculating the first order MO gradient and comparing with finite difference brings the values into much better agreement (as long as one corrects for the arbitrary MO sign convention):
I think this is the solution. If I’m missing some way to get the correct MO gradients with respect to position using the existing code, please let me know.