Is there any straightforward way to compute atomic forces from a density? Specifically, I am looking for a way to take a density represented in an auxiliary, density fitting basis set and compute Hellmann-Feynman forces on each atom.
It’s easy to get the derivative integrals in any basis, which can then be dotted with the density to get the gradients. The problem is figuring out how to handle the overlap and two electron terms. In SCF the two electrons don’t explicitly see each other so the two particle density matrix is easily expressed as products of the one particle densities; these can then be contracted with the two electron integral derivatives. These TEI derivatives are also available through MintsHelper. The TLDR answer is that the machinery all exists in terms of integral helpers, it’s just a case of thinking about what the derivative expression should look like, which depends on the nature of the density you’re handling (frozen finite width multipoles, I’m guessing?).
Maybe I’m thinking about this too simplistically, but I don’t think I need any overlap terms. I’m representing the density in a single auxiliary basis set, so I think all I need is Fi = integral(Zi * density / r^3). Am I missing something fundamental here?
Sounds very reasonable and we have the integrals that are needed. I wasn’t sure if the question was about just a standalone HIPPO-like entity or one in the presence of a QM molecule. The latter situation is doable, but harder. Just handling a standalone entity should be very easy. This Psi4Numpy tutorial gives a complete working example of how it’s done for SCF, and I suspect your problem will turn out to be simpler because of the lack of reorthonormalization gradients (the overlap terms) and the lack of two electron terms, if I’m understanding the problem correctly.
I’m just getting back to this. That tutorial is very helpful, thanks!
I see three functions, potential_grad, overlap_grad, and kinetic_grad, that look like they’re doing what I want. I realize this is probably pretty elementary, but can you spell out what each of these is doing? If I want just the Hellmann-Feynman contribution to the forces, which do I need?
potential_grad - The one-electron gradient integral associated with the electron-nuclear potential
overlap_grad - The one-electron gradient integral associated with how the perturbation changes the overlap between the LCAO-MOs, because the perturbation will change the AOs. Even Hartree-Fock theory needs this term.
kinetic_grad - The one-electron gradient integral associated with the electronic kinetic energy
I can’t say “which of these you need” because I still don’t quite understand your big picture problem. (I have less experience with things like this than @andysim, so bear with me.) For computations done in a finite basis set, the Hellmann-Feynman derivative of the Hamiltonian does produce overlap and two-electron terms. As you move the atoms, you change the basis your AOs are in, so you’ve changed the operators in the Hamiltonian themselves. The overlap terms are then necessary to make sure the MOs you’ve defined your Hamiltonian in are still orthonormal, and the two-electron terms are necessary because even though there are no nuclei involved in the electron-repulsion interaction, you have changed the two-electron operator itself by changing the AOs. The Wikipedia example of using Hellmann-Feynmann for molecular forces does not include these terms arising from a finite basis set.
Thanks for the help, @jmisiewicz!
The way I think about it, there are 3 contributions to the force.
-
The Hellmann-Feynman contribution. This is what is spelled out in the Wikipedia article you linked.
-
The finite basis set contribution. This would go away if you were using sufficiently complete basis set, but in reality you need to account for the fact that the basis functions move slightly when you move the nuclei.
-
The non-variational contribution. This come from the fact that HF theorem assumes that your wavefunction is a minimum with respect to your Hamiltonian. If it is not, then you have expensive chain rule terms to compute.
What I’m trying to do is figure out how big each of these contributions are. The big picture here is this: I have a molecular electron density represented as a linear combination of auxiliary basis functions. I want to calculate contributions 1 and 2.
Let me add some more detail on my use case since it looks like that might be helpful.
I have a machine learning algorithm that I am training to reproduce very accurate electron densities. The output of this ML model is a molecular density represented in an auxiliary basis set: density = sum(ci * Xi), where Xi are the basis functions of the auxiliary basis set and ci are the learned coefficients. I want to be able to read in this density to psi4 and compute forces from it.
Specifically, I want to start with the simple Hellmann-Feymann forces as defined in the linked Wikipedia article. I think this just looks like using computing the the OEI electron-nuclear gradient integrals, which psi4 already has machinery to to.
I understand that to the extent that my training data is non-variational and my basis set is non-complete, there will be an error. I would like to understand how big those errors are by computing each of those terms independently.
A secondary, but related goal is independent of the ML task. If I do a CCSD(T) calculation with a very large basis set, I would like to know how big the contributions to the force are from the 3 classes I listed above. My hunch is that even though CCSD(T) is non-variational, it’s density is so close to the FCI density, that the contributions from 2 and 3 will be small. I think it would be great to test this hypothesis.
It looks like for the auxiliary basis set density problem, what I actually need is ao_oei_deriv1. The documentation looks like this:
ao_oei_deriv1 ( self: psi4.core.MintsHelper , arg0: str , arg1: int ) → List[psi4.core.Matrix]
What are arg0 and arg1 here? I thought arg1 is the atom index, but putting in an integer greater than the number of atoms still gives a result.
It also appears that this method gives a result per atom that is 3 matrices, presumably x, y and z. But each of these matrices in num_basis_funcXnum_basis_func, which I did not expect. I was expecting it to return just a single num_basis_func vector (ie. the nuclear-ao gradient for each ao)?
We are quickly getting to the end of my ability to help, because I don’t know much about electron density based theories. Gradients with reduced density matrices, I can work with. It sounded like @andysim may be more knowledgeable here?
This is a case where it’s faster to look at the code yourself.
string: What type of derivatives do you want?
int: Which atom number? Because C++ is C++, array indices loop around. That’s why atom numbers grater than the number of atoms don’t (obviously) break anything.
As for return types, that’s because each one-electron integral in the Hamiltonian is associated with two AOs, so of course the derivative of an integrals will be associated with two AOs.
And yes, the three matrices are indeed X, Y, and Z.
Thanks for the explanation. It turns out that this is not the function I want, so sorry for the run-around. All that I’m really looking for is the overlap integral derivative of each individual AO on a nuclear center. I know this is not directly an operation that shows up in mainstream QM methods, but I was hoping I might be able to highjack something.
If nothing else, thanks for helping me understand the code, @jmisiewicz. I will leave a concise statement of the problem below in case anyone happens to come along with some new insight into my problem.
Problem Statement:
I want to compute the following integral to compute the force on a nucleus, i, due to an electron density represented in an auxiliary atomic basis:
F_i = sum_j(integral(Z_i * c_j * X_j / R dv) )
Here, the sum is over the j basis functions, X, and coefficients, c, and the integral is over all space.
There are two problems to be solved here:
-
Read in the auxiliary basis and coefficients. This is referenced in this post.
-
Compute the integral above.
The equation looks like you want the derivative of a single GTO w.r.t to nuclear displacement?
Is this the equation you want to solve?
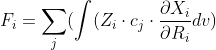
latex: F_i = \sum_j(\int (Z_i \cdot c_j \cdot \frac{\partial X_i}{\partial R_i} dv)
(embedding html code from Equation Editor for online mathematics - create, integrate and download)
The density you define [=sum(c_i * X_i)] looks like an LCAO expansion for a single MO orbital?
Hi @hokru,
Yes, everything you say is correct (way to go with the embedded LaTeX!), with the exception that it should be X_j. The density does look like a LCAO expansion of a single MO.
I thought I’d post here to say I did end up finding a (much simpler) way to compute Hellmann-Feynman Forces from psi4. I just compute the electric field at the nuclei with something like,
e, wfn = gradient('scf',return_wfn=True)
oeprop(wfn, 'GRID_FIELD')
And then multiply the resulting electric field by the nuclear charge. This works and gives the correct HF forces on each atom.
What I still do not know how to do is give my own density matrix to oeprop. That would be very cool.
oeprop reads the density matrix from the wavefunction, so you just need to set the density matrix of the wavefunction object.
This topic was automatically closed 60 days after the last reply. New replies are no longer allowed.